JAVA 라이브러리의 (java.util.Array.sort)가 사용하는 알고리즘이다. 먼저 퀵 정렬에 대해서 모르면 이 글을 읽기전에 퀵 정렬의 개념을 공부하고 이 글을 읽는것을 추천한다. Arrays.sort가 구현된 모습은 블로그에서 얘기해 주셨다.
Merge Sort는 시간 복잡도 O(N logN)을 가지지만, 실제로는 느린 모습을 보여 자주 쓰이지 않게 되었다. 사람들은 Sort알고리즘을 더 발전시킨 Dual-Pivot Quick Sort와 Tim Sort를 사용한다. Dual-Pivot Quick Sort는 삽입 정렬(Insertion Sort)와 Quick Sort를 합친 것이고, Tim Sort는 Insertion Sort와 Merge Sort를 합친 것이다.
그 전에 하나 확인하고 넘어가자. 여기서 삽입 정렬을 같이 쓰는 이유는 무엇일까? 삽입 정렬은 삽입정렬 (위키백과) 를 참고하자. 삽입 정렬에서 가장 최선의 상태는 이미 정렬된 배열을 가져왔을 때는 시간 복잡도가 O(N)밖에 걸리지 않는다. 자바에서의 Sort에서는 일정 크기를 비교하여 삽입정렬을 같이 사용하는 것으로 알고 있다. 이 글에서는 삽입 정렬이 같이 있는 형태가 아닌 말 그대로 피봇이 두개인 Dual-Pivot Quick Sort만을 다룬다.
기존의 퀵 정렬은 피봇을 1개를 기점으로 2개의 영역으로 분할해서 데이터를 정렬하는 것을 생각할 수 있다. 듀얼 피봇은 말 그대로 피봇을 2개 사용함으로써 3개의 영역으로 나눌 수 있을 것이라고 생각할 수 있다. 여기서 사용하는 피봇의 이름을 lp, rp라고 지칭하겠다.
(1) x < lp (2) lp < x < rp (3) rp < x
lp보다 작은 (1) 영역, lp와 rp의 가운데에 있는 (2)영역, rp보다 큰 (3)영역으로 나눌 수 있다. 그렇다면 이 영역을 어떤식으로 정렬을 수행할 수 있을까?
다음과 같은 연산을 반복적으로 수행하면서 정렬 연산을 수행한다.
연산
1.) 배열의 가장 왼쪽 항목은 lp로, 가장 오른쪽 항목은 rp로 설정한다.
2.) lp> rp 인 경우 lp와 rp를 바꾸어준다.
3. lp와 rp를 이용하여 다시 세 개의 영역으로 분할한다.
이를 계속해서 반복해주면 된다. 말로는 직관적으로 이해가 되지 않으니 그림과 함께 살펴보자.
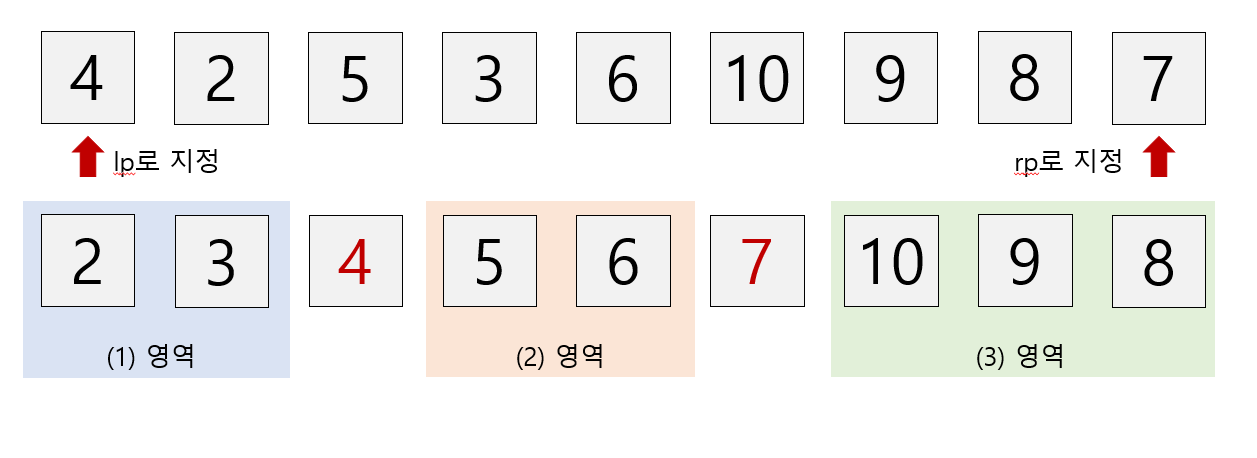
{ 4, 2, 5, 3, 6, 10, 9, 8, 7 }의 오리지널 배열이 있다고 생각해 보자.
먼저, 가장 왼쪽에 있는 4를 lp로, 가장 오른쪽에 있는 7을 rp로 지정한다.
이 때 lp와 rp의 값을 비교해주어서 lp가 rp보다 크다면 서로의 값을 바꾸어준다. 여기서는 lp가 4로 rp인 7보다 작으니 그대로 둔다.
그 다음에는 3개의 영역으로 나눈다. 3개의 영역으로 나누면서, 위에서 나눈 피봇 lp와 rp를 기점으로 각각의 영역은 포인터들과 대소관계가 유지되어야 한다.
(1) 영역은 left ~ lp-1 (2) 영역은 lp+1 ~ rp-1 (3) 영역은 rp+1 ~ right로 나누면 된다.
이제 다시 각각의 영역으로 들어가서 다시 Dual-Pivot Quick Sort를 진행해주면 된다. (1)영역과 (2)영역은 더이상 진행할 필요가 없으니 (3)영역을 확인해보자.

처음에는 lp로 10을 지정했으나, rp인 8보다 크기 때문에 서로의 위치를 바꾸어준다. 그리고 다시 세개의 영역으로 나누는데, 이때는 영역을 3개로 나눌 수 없고 1개로 나눌 수 있다.
이제 코드로 확인해보자. 코드에서 제일 중요한 부분은 l, k, g라는 변수를 사용할 것인데 여기에 대한 이해가 정말 중요하다.
l : (1)영역에 들어갈 "다음" 위치를 가리키는 변수.
g : (3)영역에 들어갈 "다음" 위치를 가리키는 변수.
k : 현재 인덱스. 적절한 영역에 들어가게 해주는 변수.
구현을 했을 때는 k가 g와 엇갈리지 않을 경우에만 반복문을 실행해주는데, 이는 rp보다 큰 값이 들어갈 자리인 g변수와 현재 인덱스인 k가 엇갈렸을 경우에는 검사가 끝이 난 것이다. 코드를 살펴보자.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
void DualPivotQuickSort(int arr[], int left, int right){
// lp : Left Pivot, rp : Right Pivot
// left > right인 경우는 배열상으로 성립이 되지 않는다.
if(left <= right){
// 양 끝의 값을 비교한다.
if(arr[left] > arr[right]){
swap(arr, left, right); // lp가 크면 lp와 rp의 위치를 바꾸어준다.
}
int lp = arr[left]; // 분할의 가장 왼쪽 값 int rp = arr[right]; // 분할의 가장 오른쪽 값
int l = left + 1;
int k = left + 1; // left+1의 원소부터 차례로 비교해준다.
int g = right - 1;
}
}
|
cs |
|
|
|
l, k, g를 left와 right와 안겹치게 하는 이유는 left는 lp로 지정하고, right는 rp로 지정한 상태이기 때문에 이를 기점으로 영역을 나누기 위함이다. 여기까지는 큰 설명이 필요 없다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
|
void DualPivotQuickSort(int arr[], int left, int right){
...
while(k <= g){ //서로 엇갈릴 때 까지
//arr[k]가 lp보다 작으면, lp보다 작은 (1)영역에 들어간다.
if(arr[k] < lp){
swap(arr, k, l);
l++;
}
...
}
|
cs |
위에서 말했듯이, k와 g가 엇갈릴 때까지 반복문을 돌린다. arr[k]가 lp보다 작다면 arr[k]와 arr[l]의 위치를 바꾸어 준다. 그리고 l을 하나 증가 시킴으로써 lp보다 작은 다음 값을 저장하기 위한 준비를 한다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
|
void DualPivotQuickSort(int arr[], int left, int right){
...
while(k <= g){ //서로 엇갈릴 때 까지
...
// lp보다 큰 (2)영역, (3)영역
else{
//rp보다 큰 (3) 영역
if(arr[k] > rp){
while(arr[g] > rp && k < g){
g--;
}
swap(arr, k, g);
g--;
if(arr[k] < lp){
swap(arr, k, l);
l++;
}
}
}
k++; // k에 대한 비교가 끝
}
}
|
cs |
k가 g보다 작아야 하는 이유는 모든 요소의 검사가 끝이 나지 않았기 때문에 바꾸지 않고 g를 낮추기 위함이다. 다음 while문은 arr[g]가 rp보다 빠져나오게 될 것이다. arr[k]는 rp보다 크기 때문에 (3)영역에 들어가야 하고, arr[g]는 반복문을 탈출한 시점에서 rp보다 작기에 (1)영역 아니면 (2)영역에 들어가게 된다.
코드에서는 k와 g를 바꾸어서 k를 (3)영역에 넣어놓고, g를 판단하는데, 위치가 바뀌었기에 다시 k를 판단해서 (1)영역과 (2)영역 중 적절한 위치에 넣는다.
그렇게 k를 하나씩 증가시켜 계속해서 확인해본다.
|
1
2
3
4
5
6
7
8
9
10
11
12
|
void DualPivotQuickSort(int arr[], int left, int right){
...
l--; g++;
swap(arr, left, l);
swap(arr, right, r);
DualPivotQuickSort(arr, left, l-1);
DualPivotQuickSort(arr, l+1, g-1);
DualPivotQuickSort(arr, g+1, right);
}
|
cs |
위와 같이 while문이 끝난다면 l과 g를 감소 시켜준다. 이는 처음에 말했듯이 l과 g는 들어갈 다음 위치를 판단하고 있는 변수이기 때문에 하나씩 줄여주는 것이다. 그렇게 l과 r을 각각 left와 right로 바꾸어주면서 lp와 rp가 적절한 위치에 가게 만들어 준다.
마지막 재귀호출은 3개의 영역으로 나누어서 Dual-Pivot Quick Sort를 계속해서 실행해나가는 것이다.
참고 블로그 : 블로그
'Algorithm > 알고리즘_개념' 카테고리의 다른 글
| [Bellman-Ford's Algorithm] 벨만-포드 알고리즘 (0) | 2021.03.31 |
|---|---|
| [Dijkstra Algorithm] 다익스트라 알고리즘 (0) | 2021.03.24 |
| [Merge Sort] 병합 정렬 (0) | 2021.03.22 |